Автор: Алек | По ту сторону Великой теоремы Ферма | Ссылки: |
(Прислано автором на сайт 26.02.2004г.)
В различные периоды своего существования, я неоднократно слышал из самых разнообразных источников и в самых разных обстоятельствах о некой великой теореме Ферма. Все величие этой теоремы, как мне показалось в то время, заключалось в неспособности математиков доказать ее в общем виде, при очевидной справедливости в частных практических решениях.
Поскольку для меня математика, как область высокоинтеллектуальной человеческой деятельности, представлялась не досягаемой, то эта проблема была сознательно отнесена мной к сфере собственной некомпетентности, и, соответственно, была автоматически исключена из круга моих интересов.
И все-таки, в какой-то момент моей жизни, обычное человеческое любопытство взяло верх, в результате чего я несколько ближе познакомился с теоремой Ферма, а так же с многочисленными проблемами вокруг нее. Удовлетворив, таким образом, свой интерес, я оставил эту тему без всякой мысли, что когда-нибудь еще вернусь к ней.
Но жизнь, порой, преподносит неожиданные сюрпризы и вносит свои коррективы в любые планы. Похоже, что это «когда-нибудь», совершенно внезапно уже настало.
Сегодня (30.10.2002 г.) ночью, совершенно неожиданно и без всяких на то видимых причин, приблизительно около трех часов, я проснулся и никак не мог заснуть вновь. До сих пор не могу понять, почему и каким образом, но вдруг я стал усиленно размышлять относительно той самой теоремы Ферма, все сведения о которой уже были давно и сознательно отодвинуты на задворки моей памяти.
Трудно сказать, какой механизм в точности был задействован, но мне кажется, что этот процесс (новый импульс автоматического интереса) возник во мне, как один из результатов моих новых представлений, формирующихся на основе неких нетрадиционных идей, внезапно вспыхнувших, и исследованиями которых я усиленно занимался в последнее время.
Наверное, именно благодаря формирующемуся новому и не совсем обычному представлению о действительном мире, мне и удалось взглянуть на проблему такого математического феномена, как теорема Ферма с совершенно другой и неожиданной стороны.
Эта другая точка зрения, скорее всего, не позволяет сформировать некое строгое доказательство теоремы в общепринятом математическом смысле. Вместе с тем, используя определенные методы, несколько отличные от математических, представляется вполне возможным получить логичные и обоснованные свидетельства не только объективной справедливости великой теоремы Ферма, но и того факта, что она действительно является Великой. Только она является Великой не в образе широко известной и достаточно старой неразрешенной математической проблемы, а в смысле глобальности и универсальности ее скрытого содержания, или же, – прекрасной и простой математической модели (трактовки) действительного физического мира (Вселенной), т.е. той самой объективной реальной действительности, которую мы пытаемся познавать.
Если быть более точным и кратким, то Великая теорема Ферма является очень удачной, красивой и достаточно простой математической трактовкой некоего глобального и универсального принципа Мироздания, - Принципа Полярности *.
Эта математическая трактовка является удачной и красивой, поскольку наиболее широко распространенный словесный образ (определение) Принципа Полярности из числа мне известных, совершенно непостижимо и до невообразимой степени согласуется с внешним математическим образом (формой) этой теоремы. Даже если это всего лишь и случайное совпадение, то оно счастливое, поскольку сыграло немаловажную роль в моих исследованиях в качестве того ключа, который сумел открыть врата новых знаний, по крайней мере, для меня.
Наиболее распространенное и доступное определение Принципа Полярности представлено в книге «Кибалион» [1], написанной неизвестными тремя посвященными в начале XX века. В этой книге кратко изложены основные идеи и принципы герметического учения.
Принцип Полярности гласит («Кибалион»):
«все двойственно: все имеет свои полюса, все имеет свою противоположность, похоже и непохоже – одно и то же, противоположности идентичны по природе, но различаются в степени, крайности сходятся, все истины – полуистины, все парадоксы можно сблизить».
Не уверен, что подобное представление глобального и универсального принципа Мироздания, способно обратить на себя внимание какого-нибудь современного исследователя. Поэтому позволю себе кратко пояснить собственными словами, приведенное несколько пространное определение Принципа Полярности:
... [все] противоположности идентичны по своей природе …, - это означает, что противоположности, по сути своей, являются одним и тем же;
… но различаются [лишь] в степени [проявления] …, - это означает, что в действительном мире противоположности всегда существуют раздельно и одновременно, как бы взаимодействуя между собой своеобразным образом. Поэтому в зависимости от того, какая из двух противоположностей в какой степени преобладает, в соответствующей степени та и проявляется, как своеобразный совокупный результат их взаимодействия;
… крайности [полюса] [противоположностей] сходятся …, - это означает, что крайние степени проявления противоположностей, называемые полюсами, по своей сути, являются одним и тем же, т.е. совпадают (сходятся). Именно феномен (свойство) схождения полюсов любых противоположностей и демонстрирует то природное единство, о котором говорилось выше.
Для большего понимания смысла и основных свойств Принципа Полярности, его образ может быть представлен графически в виде определенной символической диаграммы (рис. 1).
* Примечание: далее я буду использовать именно такое название этого принципа, хотя существует великое множество других имен и их вариаций, отличающихся по внешней форме, но которые все, по сути своей, являются образами одного и того же постижения.
Символ Принципа Полярности
Область схождения полюсов
(полюса равны и совпадают)
«ни ДА, ни НЕТ»
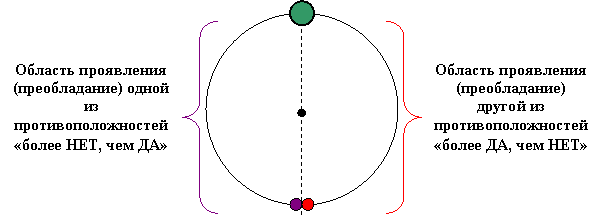
Серединная область соотношения раздельных противоположностей
(противоположности равны, но не совпадают)
«и ДА, и НЕТ»
Рис. 1
Справедливости ради, должен заметить, что здесь никакой Америки я не открываю, поскольку, как уже обращал внимание, этот принцип под тем или иным наименованием известен многим поколениям исследователей (мыслителей) с древних времен. Однако, стоит заметить, что эта известность, в подавляющем большинстве случаев, ограничивается лишь ознакомлением с его необычной и таинственной (загадочной) внешней формой, которая подобно любой одежде, периодически то исчезает из поля зрения, то вновь появляется и становится модной, но не более того. Содержание же, или глубинная сущность этого, пожалуй, самого Величайшего творения разума, до сих пор остается невостребованной тайной человеческого понимания и знаний.
Чтобы не отклоняться от главной темы изложения материалов и не загромождать их какими-то непривычными и отталкивающими «философскими» разглагольствованиями, бесполезность которых у большинства не вызывает никаких сомнений, я не стану здесь каким-то образом обосновывать справедливость и объективную истинность Принципа Полярности. Это является предметом серьезных и усиленных исследований, заслуживающих отдельного и пристального внимания. Поэтому предлагаю воспринимать его, как некий своеобразный базовый постулат или аксиому, что является вполне приемлемой общепринятой в науке практикой.
Должен сразу же признаться, что я и взялся то писать о неком другом и непривычном аспекте Великой теоремы Ферма с единственной лишь целью, - на этом конкретном и широко известном примере, как бы экспериментально, показать уникальное могущество, эффективность и силу так называемого Принципа Полярности. Поэтому, не нужно воспринимать эти материалы, как очередную попытку из многочисленных претензий на разрешение одной из загадок математической науки.
В этой работе я не раскрываю всевозможные отдельные важные свойства и следствия Принципа Полярности, а всего лишь пытаюсь на конкретном примере целенаправленно возбудить удивление, любопытство, и, в конечном итоге, - интерес, без которого эти материалы не то, чтобы понять, а и прочитать-то до конца, будет непосильной задачей.
Быть может, по крайней мере, я на это надеюсь, в результате этой сегодняшней попытки, мне удастся заинтересовать и обратить хоть какое-то внимание современных исследователей на ту, другую сторону понимания и знаний, которые, по моим представлениям, являлись достоянием человечества в прошлом, и, я искренне верю, что будут ими являться и в будущем.
Как уже отмечалось, Принцип Полярности является глобальным и универсальным законом действительного физического мира. Поэтому, как закон с глобальным и универсальным статусом, он позволяет не только выработать правильный подход в решении любой поставленной задачи, но и осуществить объективный контроль, правильности самой постановки задачи, а при необходимости, ее коррекцию (уточнение). Это уникальное свойство и особенность Принципа Полярности, представляется одной из наиболее важных, поскольку в самых разнообразных областях деятельности человека, особенно тяготеющих к абстрактным, оно, по сути, является единственным средством, не позволяющим исследователям быть увлеченными собственными иллюзиями.
Механизм реализации этого средства защиты от собственных иллюзий, заключается в неоспоримой справедливости древней мудрости и факта того, что только в правильно сформулированном вопросе (задаче), уже содержится большая часть ответа на него.
Поэтому, прежде чем приступить к решению проблем, связанных с теоремой Ферма, необходимо сначала сформулировать имеющиеся в распоряжении исходные данные, проверить их на предмет объективной корректности (правильности), и в случае необходимости, внести в них соответствующие изменения. Затем, на основании, полученных таким образом исходных данных, сформулировать окончательный вариант задачи и приступить к ее решению.
В качестве первоначальной версии исходных данных, представляется целесообразным привести оригинальную формулировку самого Пьера Ферма, написанную им на полях книги Диофанта «Арифметика»:
«Наоборот, невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата и вообще ни в какую степень, большую квадрата, на две степени с тем же показателем. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки».
Попытаемся несколько расширить и уточнить имеющиеся первоначальные исходные данные.
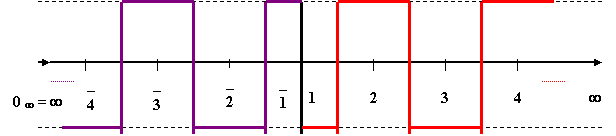
Прежде всего, представляется необходимым ввести такое понятие, как «математическое пространство» в виде бесконечного ряда положительных целых чисел, простирающегося от единицы до бесконечности (1 … JPY). По сути, бесконечный ряд таких чисел, ограниченный снизу единицей, может быть представлен графическим образом, в виде бесконечной числовой шкалы (рис. 2).
Бесконечная шкала
положительных целых чисел
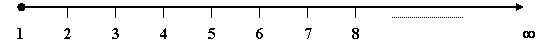
Рис. 2
Однако бесконечная числовая шкала, ограниченная снизу единицей, с точки зрения Принципа Полярности, выглядит довольно грубой частной математической трактовкой бесконечного пространства, поскольку единица и бесконечность, как крайние степени проявления единого числового ряда (его начало и конец), являются совсем не идентичными, и даже не сопоставимыми понятиями. Так, что и речи не может идти о каком-либо их схождении, как противоположных полюсов одной и той же числовой шкалы.
Кроме того, само понятие бесконечности указывает на ряд несоответствий его с рассматриваемым графическим образом (бесконечной числовой шкалой):
бесконечность, она на то и бесконечность, что не имеет границ, т.е. не может быть ограниченной;
бесконечность, как таковая, не может иметь ни начала, ни конца и ни середины;
бесконечность неделима, и, следовательно, едина.
Думаю, что, понимая все эти невообразимые (в прямом смысле) особенности свойств бесконечности, а так же явную и очевидную асимметрию и неестественную ограниченность в образе бесконечной числовой шкалы (а, возможно, и интуитивно), древние математики ввели очень своеобразное и интересное понятие «нуля». Скорее всего, нуль должен был сыграть роль некоего противовеса и гармонизатора в стремлении достичь какой-то симметрии и естественности (объективности) в образе бесконечной числовой шкалы (математического пространства).
В такой ситуации, понятие «нуль» обладает вполне определенным смыслом, существенно отличающимся от современных математических представлений. Для обеспечения гармоничного и естественного решения поставленной задачи, нуль должен представлять собой (играть роль) бесконечно малого положительного целого числа!
Следовательно, нуль (0), по сути своей, является своеобразной бесконечностью, - «нуль – бесконечностью» (![]() ). Но поскольку, одним из свойств любой бесконечности является ее единство и неделимость, то можно с определенной уверенностью утверждать, что нуль – бесконечность и бесконечность, это есть одно и тоже по своей природе, т.е.
). Но поскольку, одним из свойств любой бесконечности является ее единство и неделимость, то можно с определенной уверенностью утверждать, что нуль – бесконечность и бесконечность, это есть одно и тоже по своей природе, т.е.
![]() =
= ![]() =
= ![]() .
.
Значит, как того и требует Принцип Полярности, противоположные полюса числовой шкалы сходятся! Другими словами, в соответствии с Принципом Полярности, нуль – бесконечность и бесконечность, - это крайние степени проявления (полюса) бесконечной числовой шкалы (бесконечного математического пространства), которые сходятся или совпадают.
Таким образом, в результате применения Принципа Полярности к образу обычной общепринятой бесконечной числовой шкалы, удалось не только получить (сформировать) более истинное и совершенное его представление, но и осознать истинный смысл (суть) и назначение такого, казалось бы, тривиального математического понятия, как «нуль».
Учитывая все вышесказанное относительно вновь сформированного образа (представления) бесконечной числовой шкалы, возникает закономерный вопрос.
Что же находится (какие такие положительные целые числа) на бесконечной числовой шкале между нуль – бесконечностью и единицей?
Если учесть, что в соответствии с первоначальными исходными данными, отсутствуют какие-либо понятия (представления) о дробных и отрицательных числах, то на поставленный вопрос можно ответить только следующим образом.
Между нуль – бесконечностью и единицей имеется бесконечное множество непроявленных (никаким образом не воспринимаемых) положительных целых чисел, которые в соответствии все с тем же Принципом Полярности, являются правомерной и неотъемлемой противоположностью проявленного (действительно существующего) математического пространства (числовой шкалы).
Так, постепенно шаг за шагом, продвигаясь вперед, с помощью одного и того же Принципа Полярности, получена очередная версия образа бесконечной числовой шкалы, только на это раз, значительно расширенный до масштабов Единого математического Мира (рис. 3).
Графический образ
Единого математического Мира
I. Обобщенный вид
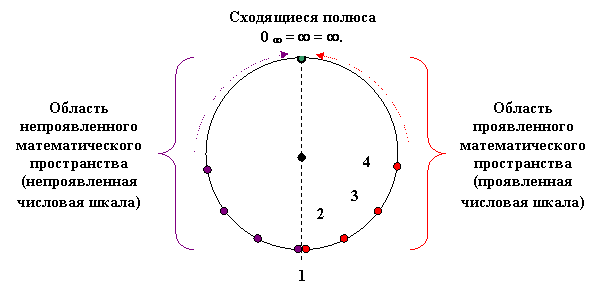
Середина
II. Частный (линейный) вид
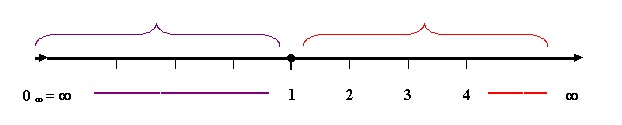
Рис. 3
Надо отметить, что в полученном образе бесконечной числовой шкалы фигурирует некое понятие ее середины, тогда как раннее утверждалось, что у бесконечности не может быть никакой середины. На первый взгляд, это обстоятельство может показаться парадоксальным и противоречивым. Ведь, рассуждая о бесконечности, невозможно оперировать такими понятиями, как начало, конец и середина. Они могут быть применимы только к конечным величинам и понятиям.
Однако, Принцип Полярности способен примирить и это противоречие. Поскольку такие понятия, как «конечность» и «бесконечность», как и любые другие противоположности, являются идентичными по своей природе. Их кажущееся противоположение (различие) друг другу, как уже отмечалось раннее на примере проявленной и непроявленной областей Единого математического мира, по сути, является относительным. И эту относительность можно достаточно легко показать на примере единицы. Хотя, для этого можно было бы использовать любое число.
Единицу можно рассматривать, как минимальное целое положительное число бесконечного числового ряда – 1, 2, 3, 4, 5, …, т.е. с точки зрения бесконечного числового ряда, единица является конечной величиной (числом).
Вместе с тем, единицу можно рассматривать, как совокупность двух числовых рядов:
1/2, 1/22, 1/23, …, 1/2n, … - это квазибесконечный нисходящий числовой ряд, ограниченный сверху числом 1/2, члены которого с возрастанием показателя n, бесконечно приближаются к нулю, или формируют «нуль – бесконечность»;
(1/2)^^1/2, (1/2)^^1/22, (1/2)^^1/23, …, (1/2)^^1/2n, … - это квазибесконечный восходящий числовой ряд, ограниченный снизу числом 1/2, члены которого с возрастанием показателя n, бесконечно приближаются к единице, или формируют «единицу – бесконечность».
В совокупности, эти квазибесконечные числовые ряды образуют единый и действительный бесконечный числовой ряд, формирующий «единицу – бесконечность», т.е. с точки зрения внутренней числовой структуры, единица является бесконечной величиной.
На рисунке 4 показано графическое представление рассмотренного совокупного бесконечного числового ряда, формирующего «единицу – бесконечность» для n = 50.
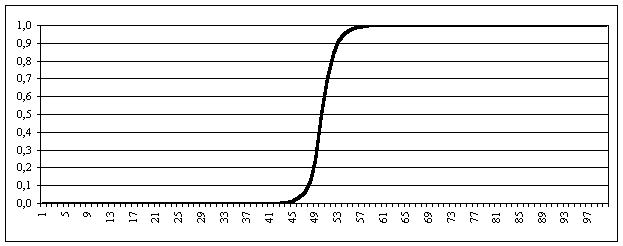
Рис. 4
Из этого графика, можно вывести достаточно любопытную вещь (особенность). Единица из конечного элемента (числа) бесконечной числовой шкалы, образующей одномерное числовое пространство, удивительным образом трансформировалась в элемент двумерного числового пространства. Причем, этот двумерный образ единицы обладает замечательными качествами. Он является конечной величиной в одном измерении (в данном случае, соответствующем оси ординат), и бесконечной величиной в другом измерении (соответствующем оси абсцисс). Так, в одном конечном элементе сочетается одновременно конечность и бесконечность.
Таким образом, с одной стороны, единица, как конечное число может иметь свои начало, середину и конец, а, с другой стороны, как бесконечность, не может иметь их. Поэтому, как ни парадоксально звучит, но любая бесконечность, в то же самое время, но в другом измерении, является конечной величиной, со всеми характерными для нее атрибутами.
Странное дело, но понятия начало, середина и конец, как несовместимые с бесконечностью, сначала помогли сформировать некое действительное (объективное) представление о бесконечной числовой шкале, а, затем, - вернуться обратно к некоему конечному образу бесконечности. Но это возвращение обратно произошло на совершенно другом качественном уровне, соответствующем осознанному представлению конечности любой бесконечности.
Если быть кратким, то можно сказать, что бесконечность является своеобразным внутренним качеством любого, с внешней точки зрения, конечного объекта (величины).
Возвращаясь к бесконечной числовой шкале, можно сказать, что очевидной серединой единой числовой шкалы и границей между проявленной и непроявленной областями Единого математического Мира, является ни что иное, как единица. Следовательно, единица, как таковая, должна быть наделена совершенно особыми качествами (свойствами), характерными, как для проявленного, так и непроявленного математического пространства одновременно.
Даже поверхностный взгляд, позволяет довольно легко обнаружить у единицы подобные свойства. Так, к проявленным свойствам единицы, можно отнести ее свойства (роль) в операциях сложения и вычитания, в которых она оказывает непосредственное влияние на формирование результата:
a + 1 = b;
a – 1 = b;
1 + 1 = 2;
1 – 1 = ![]() .
.
К непроявленным же свойствам единицы, могут быть отнесены ее свойства в операциях умножения, степени и деления, в которых она не оказывает никакого влияния на формирование результата:
a : 1 = a;
a х 1 = a;
1 х 1 = 1;
a 1 = a.
Полученная, в конечном итоге, математическая трактовка представления (образа) бесконечного пространства, мне кажется наиболее близкой к познаваемому объективному действительному Мирозданию.
Теперь необходимо ввести понятие «математического соотношения» между сформированными по определенному правилу числами (отдельными элементами математического пространства). Соотношение, по сути, является своеобразным взаимодействием между отдельными числами, сформированными по заданному закону, или же точнее, своего рода, объективной ответной реакцией Единого математического Мира на реализацию тех субъективных правил, которые были применены для формирования отдельных чисел в соотношении. Действительно, правила формирования (функции) чисел в соотношении, могут быть придуманы кем угодно и какими угодно, но свойства соотношения между ними всегда будут носить объективный характер, соразмерный воздействию (реализованными придуманными правилами).
По сути своей, математическое соотношение является субъективным инструментом воздействия исследователя на Единый математический Мир, а проявленные свойства в соотношении, - объективной и естественной реакцией этого Мира на воздействие. Очевидно, именно в этом и заключается механизм процесса познания математического Мира. В принципе, он ни чем не отличается от методологии познания физического мира или так называемой реальной действительности. Только, если в физическом мире для восприятия каких-либо свойств отдельных феноменов, мы имеем возможность использовать пять различных органов восприятия (чувств), то в математическом мире, таковых гораздо меньше. Каковы они, будет рассмотрено ниже.
Характер взаимодействия, определяется проявленными свойствами конкретного соотношения, в виде:
выполнения равенства;
не выполнения равенства, или выполнения неравенства.
Любые соотношения чисел, бесконечной проявленной числовой шкалы, их комбинаций (функций), по своей сути, является некими отдельными (частными) проявленными феноменами математического пространства (Мира), возникающими в результате воздействия на него исследователя, посредством формирования определенных правил для построения элементов того самого соотношения.
Другими словами, для того чтобы узнать, как себя поведет (проявит) камень в воде, его необходимо просто бросить в нее и внимательно наблюдать за происходящим. В данном случае камень и вода играют роль соотносимых величин, а процесс наблюдения (созерцания), - аналогичен исследованию свойств соотношения. Непосредственно же, поведение камня в воде, соответствует неким проявленным свойствам этого соотношения, выявленным в ходе его исследования.
По сути своей, математическое соотношение является тем самым, «органом восприятия» исследователя, который, пожалуй, является и единственным в сегодняшней математике. Как ни странно звучит, но, похоже, что в познании математического мира происходит то же самое, что и в физическом. А именно, вся мощь исследований направлена исключительно на изучение самых разнообразных естественных феноменов, не вдаваясь при этом в причины (механизмы) их существования. Однако, в математике существуют необычные обстоятельства, которые, не взирая на существенную ограниченность ее в восприятии (по сравнению с восприятием физического мира), вместе с тем, обеспечивают ей непревзойденное преимущество и превосходство. Но об это речь пойдет несколько ниже.
Итак, каждый математический феномен всегда способен проявиться в математическом пространстве в виде двух основных противоположных свойств, к которым относятся:
выполнение равенства в соотношении (феномене);
выполнение неравенства в соотношении (феномене).
В свою очередь, свойство, проявленное в виде выполнения неравенства в феномене, может быть дифференцированно (разделено) на два других противоположных свойства:
выполнение неравенства в соотношении, при котором левая часть этого соотношения меньше правой части;
выполнение неравенства в соотношении, при котором левая часть этого соотношения больше правой части.
Хотелось бы несколько обратить внимание на область непроявленного математического пространства Единого математического Мира, существующего между нуль – бесконечностью и единицей.
Поддавшись своему неуемному стремлению к познанию, математики всегда пытались заполнить эту кажущуюся своеобразную «пустоту» некими придуманными привычными образами, к основным из которых, например, относятся:
отрицательные числа;
дробные числа (имеется в виду 0 < a < 1);
мнимые числа и т.д.
Применяя эти числа в качестве инструмента каких-то исследований, всегда необходимо помнить, что они являются всего лишь придуманными человеком проявленными образами отдельных элементов (чисел) непроявленной области действительного Единого математического Мира. Эта предосторожность является очень важной, поскольку чрезмерное увлечение такими числами – образами, а так же непоколебимая вера в их истинность, может легко и незаметно, но вполне закономерно завести исследователя в несуществующий мир собственных иллюзий.
Назвав отдельную область математического пространства непроявленной, этим самым совсем не ограничиваются, какие бы то ни было представления о ней.
Непроявленность, является глобальным свойством, противоположным свойству проявленности. Значит, следуя путем противопоставлений, все-таки, имеется некая возможность добыть какие-то сведения относительно непроявленной области в целом, и ее отдельных элементов в частности.
И первым таким глобальным свойством области непроявленного является то, что она и называется непроявленной, поскольку никакими образами (в обычном понимании) не может быть проявлена (представлена).
Здесь необходимо обратить внимание на ключевое понятие «образ», которое является единственным критерием в разделении Единого математического Мира на две противоположные области. Следовательно, существует такое же, но противоположное, по сути, понятие «не-образ», с помощью которого в непроявленной области и формируются все представления. Так вот, с позиций этих самых представлений в «не-образах», об области проявленного пространства можно рассуждать, только противопоставляя его своему известному и привычному непроявленному миру.
Другими словами, понятия «проявленность» и «непроявленность», являются не только очевидными противоположностями одного и того же Мира, но и относительными понятиями.
С позиций непроявленной области, представляющейся такой ясной и понятной в «не-образах», проявленная область выглядит совершенно загадочной, нереальной и как бы невидимой, поскольку просто не существует в этих самых «не-образах».
С позиций же проявленной области, вся картина представлений об обеих областях выглядит с точностью до наоборот.
Правильно понимая такую относительность представлений о проявленной и непроявленной областях Единого математического Мира (пространства), можно вполне обоснованно утверждать, что совершенно невозможно обладать (создать) какими-то «образными» представлениями о непроявленном. Поэтому любая попытка выдумывания (рисования) таких «образов», уже сама по себе является в определенной степени ошибочной и ущербной.
Вместе с тем, такое положение дел, не должно загонять исследователей в тупик, в своем стремлении познания этого загадочного и таинственного непроявленного математического пространства.
Не смотря на то, что невозможно иметь какие-либо представления в «образах» относительно непроявленного, а так же на то, что это отсутствие последних создает автоматическое впечатление отсутствия и самих предметов исследования (познания), вместе с тем, изучение непроявленного мира, все же, возможно.
И «квазиобъектами» такого возможного познания непроявленного мира, являются ни непосредственно «не-образы», о которых непосредственно в отдельности объективно невозможно что-либо судить, а только, если можно так сказать, - свойства этих самых «не-образов».
Значит, предметом исследований непроявленного мира, могут быть лишь отдельные свойства его отдельных элементов, представление о которых можно сформировать на основе воспринимаемых и известных аналогичных свойств отдельных образов проявленного мира.
Для того, чтобы правильно воспринять и понять сказанное, рассмотрим небольшой и простой пример. Однако, прежде, чем приступить к рассмотрению каких-либо примеров, введем соответствующие понятия и символы, позволяющие их воспринимать:
М – Единый математический Мир;
м – проявленная область Единого математического Мира;
_
м - непроявленная область Единого математического Мира;
a, b, c, … - отдельные «образы» (числа) проявленного мира;
_ _ _
a, b, c, … - отдельные «не-образы» (числа) непроявленного мира.
Пример 1.
Пусть a, является n-ным членом ряда положительных целых чисел, например:
2 – второй член числового ряда;
5 – пятый член числового ряда и т.д.
_
Тогда, если a n , обладает свойством четности, то a n , будет обязательно обладать свойством нечетности.
Другими словами, если привычная всем двойка, в проявленном математическом мире обладает свойством четности и является главным критерием в определении этого свойства, то в непроявленном мире, аналогичная ей «двойка», «не-образ» которой недоступен, обладает свойством нечетности. Попробуйте представить себе подобную нечетную «двойку», и перед вами возникнет неразрешимая проблема.
Необходимо обратить пристальное внимание на очень важное и основополагающее обстоятельство (свойство), которое является своеобразным ключом к пониманию всего здесь излагаемого.
Двойка проявленного мира, и, соответствующая (аналогичная) ей двойка непроявленного мира, являются всего лишь относительными понятиями отдельных глобальных областей (проявленного и непроявленного), но Единого, по своей сути, математического Мира. И с позиций этого самого Единого математического Мира, существует единственное и абсолютное понятие двойки.
С одной стороны, эта мировая единая (абсолютная) двойка, должна обладать свойствами двоек обеих областей, т.е. она одновременно является четной и нечетной. Однако, с другой стороны, наличие противоположных свойств в одном и том же едином, отдельном элементе теряет всякий смысл своего раздельного существования. Действительно, что можно сказать о четности, проявленности и т.п. единой (абсолютной) двойки? Ничего! Эти свойства для нее, как бы не существуют, они исчезают, растворяются в своем единстве или поглощаются Единым, неделимым и бесконечным математическим Миром.
И теперь о самом фантастическом.
На основе результатов, полученных в рассмотренном примере, можно сделать удивительный вывод о том, что все свойства отдельных «образов» и «не-образов» двух миров (проявленного и непроявленного), растворяются и поглощаются Единым математическим Миром, тем самым, устраняя всякое различие между ними.
Другими словами, с абсолютной позиции Единого математического Мира, никаких отдельных элементов, объектов или представлений просто не существует, т.е. любые числа проявленных и непроявленных математических областей, являются совершенно тождественными (одним и тем же).
Однако, даже в условиях таких глобальных и фантастических метаморфоз, все же, возможно составить (сформировать) некое представление о Едином математическом Мире. Только такое представление будет единственным и ни с чем несопоставимым, как говориться по определению.
Думаю, что не трудно догадаться, что этим абсолютным и единственным представлением Единого математического Мира является ЕДИНИЦА.
Значит, образ единицы, как середины бесконечной числовой шкалы или границы противоположных раздельных областей (проявленной и непроявленной), со всеми своими отдельными «образами» и «не-образами» (числами) является, по сути своей, воплощением Единого математического Мира, т.е.
_
М = м + м = 1.
Подобная тождественность образов Единого математического Мира и конечного числа – середины этого самого Мира, не должно вводить умы в заблуждение и смятение перед лицом очередного кажущегося парадокса. Ведь, раннее уже установлено, что в зависимости от «измерения» единица может быть, как конечной величиной, так и бесконечностью. Это уникальное свойство единицы, представляется очень важным.
Наверное, именно такой смысл вкладывали в образ единицы пифагорейцы и другие выдающиеся древние математики.
Из предыдущих рассуждений со всей очевидностью следует, что отдельные свойства элементов проявленной области, по сути, однозначно и объективно определяют характер аналогичных отдельных свойств элементов в непроявленной области. Стоит заметить, что справедливым будет и обратное утверждение. Другими словами, отдельные аналогичные свойства элементов («объектов» и «не-объектов») обеих областей, взаимоопределяют и взаимовлияют друг на друга, что, в общем-то, и является тем самым скрытым от обычного взора механизмом или причиной, которые образует естественный, гармоничный и устойчивый Единый математический Мир.
Человеку, в его обычном восприятии (естественных математических образов или чисел), непосредственно доступна только проявленная область Единого математического Мира. Поэтому, ограничиваясь в своем познании только рамками этой области, со всеми его объектами и феноменами, он объективно никогда не сможет понять Единый математический Мир, поскольку «причины» наблюдаемых феноменов, скрыты от нашего взора в непрявленной области этого самого Мира.
В этой непростой и, казалось бы, безвыходной обстановке, огромную роль сыграло то необычное обстоятельство (особенность математики), которое, не взирая на существенную ограниченность восприятия математического мира, вместе с тем, обеспечивает ей непревзойденное преимущество и превосходство перед физическим миром. На это уже обращалось внимание, и теперь настало время несколько пояснить это обстоятельство.
Создав определенный набор средств (методов и способов) логического построения (доказательств) различных математических соотношений, исследователь получает практически неограниченные возможности изучения отдельных феноменов во всей своей целостности и единстве, т.е. в «пределах» всего Единого математического Мира. Поэтому, не смотря на то, что в математическом мире, восприятие человека (исследователя) ограничено одним единственным «органом», вместе с тем, его возможности поистине не ограничены. Подобное восприятие способно объять разом весь бесконечный Единый математический Мир.
Другими словами, в отличие от мира физического, где человек располагает пятью органами чувств, но ограниченными по своим возможностям, в математическом - он располагает всего лишь одним «чувством». Однако, возможности у этого «чувства» практически не ограничены.
Что лучше, пять ограниченных чувств или одно неограниченное, - это еще вопрос?
Но мне кажется, что лучше будет, если не задавать подобных бесполезных вопросов.
Гораздо более полезным и естественным представляется полноценное использование всех имеющихся возможностей восприятия человека. Поэтому, наверное, будет правильным отнести это «математическое восприятие» человека (разума) к его особому «шестому» чувству.
Стоит обратить внимание на то, что «шестое» чувство человека является делом рук (результатом деятельности) самого человека, т.е., по сути, оно является рукотворным. Думаю, что именно в этом качестве и заключается его неоспоримая и несравнимая познавательная мощь.
Вместе с тем, как это всегда бывает, наряду с познавательной (созидающей) мощью, «шестое» чувство обладает, и при соответствующих условиях может обернуться в опаснейшую разрушительную мощь. И определяются эти условия «качеством» или достоверностью «шестого» чувства. Ведь, поскольку оно является продуктом особой абстрактной деятельности человека, то имеется некая вероятность недостоверного (искаженного) его функционирования.
Следовательно, «шестое» чувство (математическое восприятие) человека, может быть полезным и ценным, только если оно будет сформировано с соблюдением неких естественных и объективных закономерностей (принципов), обеспечивающих его достоверное функционирование.
И первое, что приходит на ум после такого утверждения является тем, что эти самые принципы должны быть точно такими же, как и те, на основе которых функционируют все наши естественные и привычные органы чувств. А это, в свою очередь, подтверждает основную идею и цель данной работы. Поскольку, думаю, что Принцип Полярности, который выступает в качестве сердцевины этих исследований, как раз и является такой естественной и объективной закономерностью.
Подобные рассуждения подталкивают к мысли об удивительном и таинственном сходстве или родстве между физическим и математическим мирами. А, такая постановка вопроса (точка зрения), может в корне изменить место и роль математической науки в едином процессе развития человечества. Или, по крайней мере, позволит осознать и правильно понимать свое ведущее положение среди других областей человеческих знаний.
Только при условии естественности и объективности, математическое восприятие, как рукотворное, имеет право занять свое достойное место в ряду других природных (даденных) чувств человека. До этой поры, все, что связано с подобным восприятием, будет более напоминать игру самыми разнообразными придуманными «игрушками», которые в неумелых руках «дитя – человечества», могут быть как полезными, так и исключительно вредными (опасными).
Наверное, с позиции подобных рассуждений (установок) и следовало бы начинать эту работу. По крайней мере, в этом месте наиболее ясно просматриваются те интуитивные посылки, которые так или иначе, но привели меня к попытке использования теоремы Ферма для демонстрации Принципа Полярности. Однако, все обдумав и взвесив еще раз, я посчитал целесообразным и полезным оставить последовательность изложения материала неизменной. Ведь, в конечном счете, измененный порядок изложения мне только кажется предпочтительным (лучшим), тогда как, выдерживаемый существующий, является той самой реально опробованной «дорогой», по которой удалось уже пройти единожды.
Итак, применяя самые разнообразные методы и способы логического построения (доказательства) различных математических соотношений, исследователи научились не только сосредотачивать свое внимание на каком-то определенном феномене, но и – охватывать своим «взором» этот феномен во всей его целостности и единстве в «пределах» бесконечного Единого математического Мира.
Однако, вся история развития математической науки, убедительно показывает, что, отнюдь, не всегда исследователям представляется возможность реализовать имеющиеся в распоряжении методы для достижения подобных желаемых результатов, т.е. не всегда можно полноценно пользоваться своим математическим восприятием (чувством) в процессе познания математического мира.
В поисках выхода из многочисленных подобных ситуаций, удалось обнаружить (скорее всего, случайно или интуитивно) удивительную способность Единого математического Мира. Оказывается, что существует возможность оказывать воздействие на весь этот мир сразу одновременно, во всей его целостности и единстве. Естественной ответной реакцией Единого математического Мира (пространства) на такое глобальное воздействие, будут некие своеобразные изменения в проявлениях его феноменов. Характер этих изменений заключается в том, что отдельные свойства, качества или элементы одного и того же математического феномена начинают по-другому проявляться в измененных условиях математического пространства. Именно эти изменения в проявленных свойствах одного и того же феномена, могут способствовать не только достижению поставленной цели (доказательству), но и – выработке новых логических методов для реализации различных доказательств.
Думаю, что, по крайней мере, существует как минимум два способа глобального воздействия на Единый математический Мир, в которых, по сути, реализуется механизм изменения образа (представления) бесконечной числовой шкалы. На мой взгляд, достичь этого можно, либо вводя какие-то новые разновидности чисел в ее существующую структуру (форму или топологию), либо изменяя ее линейную форму на какую-нибудь другую, например, треугольную.
Не смотря на всевозможные трансформации Единого математического Мира, он по-прежнему и всегда остается все тем же единственно возможным Единым математическим Миром. Исключительная ценность таких трансформаций заключается в том, что у исследователя появляется дополнительная возможность использования своего единственного математического восприятия с различных точек зрения, в которых один и тот же мир смотрится совершенно по-разному.
В какой-то мере этот процесс напоминает изучение куба по его тени. По форме лишь одной единственной тени, вряд ли кто-нибудь сможет понять такую фигуру. Скорее всего, он будет воспринят, как квадрат, прямоугольник или какой-нибудь выпуклый пятиугольник. Только путем вращения куба в лучах света, обеспечивая, тем самым, восприятие в форме теней его скрытых свойств, в совокупности позволяют понять этот феномен во всей своей целостности и единстве.
Таким образом, глобальные воздействия на Единый математический Мир, позволяют, как бы вращать его перед своим «взором» в поисках необходимого ракурса, позволяющего исследовать (доказать) конкретный отдельный математический феномен.
На бесконечной числовой шкале существует огромная область пространства, которая не может предстать перед «взором» исследователя ни в каком из мыслимых образов, - это область непроявленного математического пространства.
Думаю, что эту область невозможно раз и навсегда заполнить какими-то определенными привычными образами (числами), поскольку ни одни из них не способны обладать всей совокупностью свойств, характерных для чисел этой области. Иначе, они были бы представимы в обычных образах, и ничем не отличались бы от них.
Поэтому, подобные образы чисел непроявленной области математического пространства, могут быть использованы лишь ограничено, только для решения определенной группы конкретных задач.
Отрицательные, дробные (имеется в виду 0 < a < 1), комплексные и другие числа, уже существующие, а так же те, которые появятся (возникнут) в будущем, - все они, по сути своей, являются различными образами одних и тех же действительных (истинных) непроявленных чисел.
Возможно, что именно по причине единого родства всех этих чисел, которые сегодня считаются различными, математическая наука еще преподнесет ряд сюрпризов и головоломок.
Если воздействия на Единый математический Мир способом введения новых разновидностей чисел, не взирая на некоторые возможные сложности восприятия, еще как-то можно принять. И, вся история развития математической науки, является тому убедительным свидетельством, поскольку случалось это не один раз.
Относительно же, высказанного утверждения, о возможности воздействия на Единый математический Мир способом изменения его формы (топологии) представления, думаю, что оно вызовет у большинства исследователей серьезные трудности и проблемы с воображением подобной химеры. Хотя бесконечная числовая шкала, круговая бесконечная шкала, бесконечная двумерная плоскость и бесконечное трехмерное пространство, - все они являются именно такими разновидностями формы представления одного и того же Единого математического Мира.
В конечном счете, уже только наличие указанных разновидностей форм представления Единого математического Мира, допускает саму возможность формирования неких его топологических (геометрических) образов. И треугольник, в этом смысле, ничем не хуже, например, прямой линии, разве что несколько непривычен в этом образе и кажется невообразимым, поскольку достаточно трудно представить себе «бесконечный треугольник», каковым является Единый математический Мир.
Попытаемся определить этот самый «бесконечный треугольник», который может выступить в роли образа бесконечной числовой шкалы.
Таким треугольником является некий абстрактный универсальный (абсолютный) треугольник, сочетающий в себе одновременно наряду со всеми возможными разновидностями формы, так же и все возможные величины длин его сторон, т.е. от единицы до бесконечности.
Подобный треугольник можно вообразить себе как бы резиновым, у которого величины длин сторон могут свободно изменяться в интервале от единицы до бесконечности, а его форма – от максимально остроугольной до максимально тупоугольной. По сути своей, этот треугольник является воплощением бесконечного числа всех возможных треугольников, поэтому, может быть, так же вообразим в виде особого «динамического» треугольника, пребывающего в процессе постоянной и бесконечной трансформации от одной его разновидности к другой. Причем, интенсивность (скорость) такого процесса столь высока, что все эти разновидности треугольника как бы присутствуют в нем все разом и одновременно.
Если сопоставить бесконечную числовую шкалу с таким абстрактным «бесконечным треугольником», то бесконечные возможные вариации его формы и размеров, приведут к тому, что вся числовая шкала окажется сплошным образом покрыта числовыми значениями всевозможных длин его сторон. Особенностью такого покрытия (формирования) бесконечной числовой шкалы заключается в том, что оно будет происходить не отдельными числами, а определенными тройками чисел, связанных между собой соответствующим образом, в зависимости от формы треугольника.
Думаю, является совершенно очевидным фактом, что любое отдельное число бесконечной числовой шкалы может быть представлено в виде бесконечного количества разнообразных по форме треугольников. И каждый такой треугольник, помимо необходимого отдельного числа, представляет (дает) еще два дополнительных числа, жестко связанных с ним формой треугольника.
Необходимо обратить особое внимание на последнее обстоятельство, - появление самых разнообразных взаимосвязанных между собой числовых троек в «пространстве» бесконечной числовой шкалы.
Конечно, подобная связь между аналогичными тройками чисел существует и в представлении бесконечной числовой шкалы. Однако, только ее треугольный образ позволил в ярко выраженном (явном) виде увидеть и понять раннее скрытые закономерности (суть) этих связей.
Другими словами, треугольное представление Единого математического Мира (бесконечной числовой шкалы), позволило взглянуть на этот самый мир под совершенно иным углом зрения (ракурсом), позволяющим рассмотреть (вскрыть) его некие раннее непроявленные отдельные свойства.
Таким образом, с помощью введения в Единое математическое пространство новых разновидностей чисел (воздействуя на его содержание), или придания ему образа некой новой геометрической формы (воздействуя на его форму), можно сформировать разнообразное множество представлений одного и того же, по сути, Единого математического Мира. А эти представления, в свою очередь, способны содействовать успешному решению (доказательству) самых разнообразных сложнейших задач.
О способах, с помощью которых могут быть восприняты те или иные свойства какого-либо отдельного математического феномена, а так же о возможностях оказания воздействий (влияний) на проявление этих самых свойств, пойдет речь в последующем небольшом примере – исследовании.
Пример 2.
Рассмотрим такой математический феномен, как четность чисел.
Все отдельные числа бесконечной числовой шкалы могут обладать одним из двух противоположных качеств, - быть четным или нечетным, т.е. они могут быть отнесены к группе (множеству) либо четных, либо нечетных чисел.
Как уже отмечалось раннее, причины свойств четности (четности и нечетности) у объектов (чисел) проявленной области, пребывают и сокрыты в непроявленной области, как, впрочем, и наоборот. Этот механизм, достаточно наглядно представлен на рисунке 5.
Из этого простого графика видно, что свойство четности и нечетности аналогичных чисел в обеих областях, как бы находятся в противофазе, или центрально симметричны относительно единицы (естественной середины). Единица же, сама по себе, одновременно является и четной, и нечетной, в зависимости от позиции (области), с которой она рассматривается.
«Чет»
«Нечет»
Рис. 5
Подобная центральная симметрия отдельных аналогичных свойств, является объективным и неотъемлемым условием естественной гармоничности и устойчивости Единого математического Мира. Именно только с позиции отмеченной естественной гармонии Единого математического Мира, такой отдельный феномен, как «четность», и может существовать в нем, или не существовать, будучи поглощенным и растворенным им же.
Этот же график указывает еще на одну особенность отдельных математических феноменов. Заключается эта особенность в том, что один и тот же отдельный феномен, в пределах одной и той же области, может проявлять свои противоположные свойства. Таких реверсов противоположных свойств отдельного феномена в одной и той же области, может быть от единицы до бесконечности, как, например, в случае с феноменом четности чисел. Однако, самым главным, гармонизирующим или балансирующим реверсом, всегда является тот, что происходит на границе раздела двух противоположных областей, т.е. в единице.
Поиск точек реверса свойств отдельных феноменов, может представлять определенный интерес и практическую ценность. Вместе с тем, необходимо отметить, что, скорее всего, такой поиск не всегда возможен. Например, относительно феномена четности, можно сказать, что такие точки реверса оказываются неявными (невыраженными в явном виде), не смотря на то, что они пребывают все же в проявленной области, и их количество бесконечно.
Если понятие четности несколько расширить, путем распространения этого свойства на дробные числа, при этом, допустив бесконечное множество градаций проявления этого свойства, то точки реверса сразу же обнаружатся в явном виде, т.е. функция феномена четности, например, между непроявленной и проявленной тройкой примет вид, представленный на рисунке 6.
При этом, на интервале между обычной двойкой и тройкой свойства функции четности можно охарактеризовать следующим образом:
2 – абсолютно четно;
2, 1 – менее четно, чем 2, но при этом более четно, чем нечетно;
…;
2,5 – и четно, и нечетно одновременно;
…;
2,9 - менее нечетно, чем 3, но более нечетно, чем четно;
3 – абсолютно нечетно.
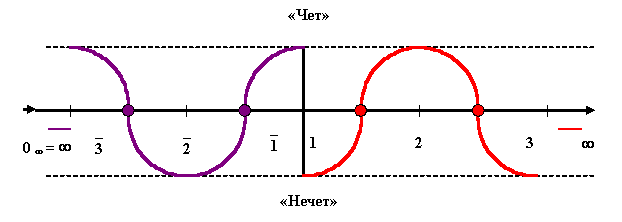
Рис. 6
Изменения в трактовке феномена четности чисел привели к тому, что его функция будет иметь несколько другой внешний вид и характер. В частности, что представляется очень важным, свойства многочисленных реверсов этой функции (феномена), из разряда неявных перешли в явный (проявленный) вид. Поэтому, появилась целая группа (разновидность) конкретных отдельных чисел, которые одновременно являются и четными, и нечетными числами.
Здесь, воочию можно наблюдать, как введение некой дискретности в понятие четности чисел, что равносильно распространению этого феномена на обычные дроби, очень наглядно повлияло на характер его проявленных свойств. Удалось совершенно с другой точки зрения взглянуть на исследуемый математический феномен, при этом он приобрел более ясные и четкие черты. И произошло это, прежде всего, поскольку, несомненно, присутствующие в первоначальном (обычном) представлении функции этого феномена, неявные (мнимые или виртуальные) точки реверса, трансформировались в явные.
Стоит обратить особое внимание на то обстоятельство, что точки реверса и в том, и в другом представлении математического феномена четности чисел, оказываются тесно взаимосвязанными, т.е., по сути своей, они являются одними и теми же точками реверсами, только представшими в разных видах (явном и неявном) перед взором исследователя.
Рассматривая характер точек реверса проявленных свойств какого-либо математического феномена, можно прийти к следующему очень значительному и интересному их свойству (качеству).
Поскольку речь идет об одном и том же едином математическом феномене, а точнее, об одном из двух возможных его проявленных свойствах, то точки реверса, как таковые, этих самых противоположных свойств, могут быть только однотипными, т.е. либо явными, либо неявными. В противном случае, между ними так же должны существовать некие другие точки реверса (как бы, реверс точек реверса) такого свойства, как «явный» и «неявный» вид первичных точек реверса. А подобное утверждение не может иметь какого-либо смысла, поскольку допускает существование понятия, противоположного понятию точке реверса, что уже само по себе абсурдно, поскольку возможно лишь при наличии в любой паре противоположностей еще и третьей противоположности (составляющей).
Таким образом, в пределах одной и той же области математического пространства (проявленной или непроявленной), все возможные точки реверса противоположных свойств какого-либо из математических феноменов, могут восприниматься только в явном, или только в неявном виде (или вообще отсутствовать), в зависимости от формы или способа представления Единого математического Мира. При этом, не зависимо от формы или способа его представления, а так же видов восприятия в них точек реверса, количество последних не изменяется. Так, что каждой точке реверса в одном из представлений Единого математического Мира, всегда соответствует в том или ином виде только одна единственная соответствующая точка реверса в его другом представлении.
Значит, по сути, для того чтобы познать и понять какой-либо математический феномен, необходимо, прежде всего, определить количество и закономерности распределения точек реверса его проявляемых свойств.
Однако, не все обстоит так просто, как кажется. Если некую точку (точки) реверса свойств отдельного феномена, в явном или неявном виде, представляется возможным определить практическим путем (эмпирически), то решение задачи о количестве таких точек и их распределении, подобными методами никак не может быть достигнуто.
И все же, такая возможность существует. А позволяют реализовать эту возможность те выводы, к которым привели проведенные здесь исследования.
Впрочем, любой, по истине, мыслящий исследователь, дочитав до этого места, вполне будет способным самостоятельно и без всякой помощи показать справедливость Великой теоремы Ферма.
Думаю, что не стоит лишать себя подобной возможности и удовольствия, поскольку, на мой взгляд, только самостоятельное открытие истин, пусть даже уже давно и большинству известных, единственно и являются самым ценным приобретением (индивидуальным достоянием) в процессе любого познания.
Мне кажется, что обязательно найдутся люди, которые, какими бы занятыми не казались, а, по сути, из-за собственной лени, могут сразу же приступить к ознакомлению именно с этим разделом моей работы, надеясь на легкое и быстрое приобретение каких-то знаний, в лучшем случае. В худшем же случае, по крайней мере, будет удовлетворено их простое человеческое любопытство, а представленные здесь идеи, будут автоматически отнесены к разряду больного воображения очередного дилетанта. Думаю, что по большей части, именно так все и произойдет.
Я обращаюсь, прежде всего, к подобным людям, и хочу их предостеречь от скоропалительных и поверхностных суждений. Необходимо всегда помнить, что только величина затраченных усилий, определяет результаты любого развития, в том числе и понимания.
Этот раздел, по своей сути, является лишь отдельной (частной) попыткой практической реализации, того глобального и универсального понимания, который кратко изложен в предыдущих материалах.
Сам по себе, в отдельности и отрыве от основной и главной части материалов, этот раздел не может создать условий и позволить приобрести какое-либо понимание относительно излагаемых здесь идей. А без какого-либо понимания этих идей, представляется совершенно бесполезным обладание их знанием, даже относительно столь великой теоремы.
Для тех, кто начал свое чтение с этого раздела, позволю себе повториться.
Мне кажется, что не стоит лишать себя уникальной возможности и удовольствия в виде попытки самостоятельного разрешения проблемы Великой теоремы Ферма, поскольку только самостоятельное открытие истин, пусть даже давно и всем известных, единственно и является самым ценным приобретением (индивидуальным достоянием) в процессе любого познания.
Последующие материалы более предназначены для исследователей, которые пожелали получить какие-либо убедительные свидетельства относительно справедливости изложенных здесь идей. Что, несомненно, будет являться свидетельством появления того интереса, возбуждение которого единственно и является целью моих изложений.
В отличие от общепринятых представлений, мне кажется, что Великая теорема Ферма, как отдельный математический феномен проявленной области Единого математического Мира, имеет гораздо более широкую трактовку, нежели существующая.
Думаю, что в наиболее широком смысле, теорема Ферма определяет закономерности проявлений соотношения между суммой одинаковых степеней двух произвольных чисел и той же степени третьего числа, в зависимости от СТЕПЕНИ, т.е.:
(a n + b n) и c n,
где a, b, c, n – положительные целые числа.
Тогда эту теорему можно сформулировать следующим образом:
- для любых произвольных чисел a и b , всегда найдется такое число c, что справедливым будет равенство:
a + b = c, при n = 1.
- только для определенных двух чисел a и b , может найтись такое число c, что справедливым будет равенство:
a 2 + b 2 = c 2, при n = 2.
Причем, числа a, b и c образуют строго определенные тройки в бесконечном проявленном числовом пространстве. Для всех других, не входящих в состав указанных троек чисел a и b, не существует такого числа c, чтобы выполнилось указанное равенство. Следовательно, для таких чисел справедливым будет неравенство:
a 2 + b 2 1 c 2, при n = 2.
- для любых произвольных чисел a и b , никогда не найдется (не существует) такое число c, что справедливым было бы равенство:
a n + b n = c n, при n > 2.
Следовательно, всегда справедливым будет неравенство:
a n + b n 1 c n, при n > 2.
Подобная трактовка теоремы Ферма в наиболее общем виде, уже сразу же позволяет заключить, что при n = 2, происходит реверс свойств, проявляемых в рассматриваемых соотношениях, в зависимости от СТЕПЕНИ!
Подобное утверждение основано на том, что именно при n = 2, феномен соотношения объектов может быть проявлен как в форме (образе) равенства, так и – неравенства. А такой особенностью может обладать только точка (в данном случае степень) реверса проявляемых свойств.
Значит, остается только показать, что этот очевидный реверс, проявляемых свойств феномена соотношения при n = 2, является единственным для всего бесконечного проявленного числового пространства.
Думаю, что боле, чем 350-летнего периода бездоказательного существования Великой теоремы Ферма является достаточным, для того, чтобы сделать вывод об отсутствии существования в явном виде каких бы то ни было свойств этого математического феномена, позволяющих показать его справедливость (истинность). Многочисленные безуспешные попытки доказательства этой теоремы на протяжении значительного периода времени, настоятельно указывают на то, что в обычном (привычном) представлении бесконечного числового пространства, скорее всего, отсутствует сама возможность подобного доказательства, подобно отсутствующей в явном виде точке реверса между четными и нечетными числами.
Поэтому, для достижения этой цели, понадобится тем или иным путем трансформировать (изменить представление) Единый математический Мир таким образом, чтобы в явном виде проявились закономерности естественных и объективных связей между любыми тройками чисел, принадлежащих бесконечной числовой шкале.
На основании полученных результатов, нетрудно догадаться, что таким, пожалуй, возможным единственным представлением Единого математического Мира, является его треугольный образ, основные свойства и особенности которого были рассмотрены в наиболее общих чертах раннее. Возможно, что с помощью такого воздействия на Единый математический Мир, удастся обнаружить некие, изначально неявные (невыраженные) аспекты исследуемого феномена, которые смогут способствовать его полноценному познанию (доказательству).
А, поскольку, треугольная форма представления Единого математического Мира, позволяет лишь изменить точку зрения на него, оставляя неизменной его суть, то результаты, полученные таким образом, автоматически будут справедливыми (истинными) для того же, единственно возможного, Единого математического Мира, чьим образом (отражением) является любое его представление.
Попытаемся применить эту новую технологию для решения конкретной очень сложной задачи. Что может быть лучше подобного серьезного испытания (опыта)?
Пусть треугольное представление Единого математического Мира (бесконечной числовой шкалы), имеет длины сторон (далее стороны), соответствующие числам a, b и c.
В зависимости от величины угла между сторонами a и b, треугольник может быть следующих видов:
остроугольный;
прямоугольный;
тупоугольный.
Применяя Принцип Полярности к всевозможным формам треугольника, учитывая, что «остроугольность» является явной противоположностью «тупоугольности» в феномене формообразовании любого треугольника, можно предположить, что «прямоугольность» его формы является естественной серединой и явной точкой реверса.
Действительно, максимально остроугольный и максимально тупоугольный треугольники вырождаются (сходятся) в один и тот же объект, - отрезок линии. Поэтому, с точки зрения Принципа Полярности, представленные виды треугольников являются полной и естественной единой группой (набором) всевозможных его форм.
Таким образом, применив треугольное представление образа бесконечной числовой шкалы, мы автоматически приобрели еще одно свойство в рассматриваемом феномене, - это форма треугольника. Причем, полученное в распоряжение формообразующее свойство треугольника, обладает ярко выраженной (явной), очевидной и единственной точкой реверса в виде его прямоугольной формы.
Наличие у одного и того же, треугольного, представления бесконечной числовой шкалы, двух раздельно воспринимаемых свойств со своими точками реверса, интуитивно указывают на то, что, возможно, именно прямоугольная форма треугольника (как наиболее глобального свойства математического пространства) и является воплощением своеобразной единой точки реверса всех возможных проявляемых свойств в этом образе. Ведь, в конечном счете, именно треугольник лежит в основе такого представления «безликой» бесконечной числовой шкалы.
Проведем небольшое вспомогательное исследование некоторых простых свойств, разнообразных типов треугольников.
Пожалуй, не требует отдельного рассмотрения, одно из известных со школьной скамьи свойств любого треугольника, заключающееся в том, что
сумма длин двух любых сторон всякого треугольника, всегда больше длинны его третьей стороны:
a + b > c.
Следуя этим путем дальше, можно достаточно легко прийти к тому, что, оказывается, если возвести во вторую степень (n = 2) члены, приведенного выше неравенства, то вопрос с возможными вариантами проявления свойств в соотношении, не решается так однозначно и просто, как для первой степени (n = 1).
В этой ситуации, для каждого из возможных видов треугольника, будет справедливым исключительно свое отдельное свойство в исследуемом соотношении сторон треугольника (Таблица 1).
Таблица 1
Остроугольный | Прямоугольный | Тупоугольный |
a 2 + b 2 > c 2 | a 2 + b 2 = c 2 | a 2 + b 2 < c 2 |
Позволю себе, не приводить здесь строгое доказательство столь очевидного факта.
Анализируя полученные соотношения с позиции Принципа Полярности, можно убедиться в том, что прямоугольный вид треугольника действительно является точкой, где происходит своеобразной реверс его формы с остроугольной, на тупоугольную. А вместе с реверсом его формы, осуществляется и реверс проявленных свойств феномена соотношения сторон треугольника для второй степени (n = 2).
Значит, прямоугольный вид треугольника является не только возможным единственным реверсом такого его свойства, как форма, но и может выступать в роли своеобразной области, в которой наиболее возможно существование (пребывание) точек реверса и других свойств треугольника, в том числе, и соотношение его сторон.
На подобный вывод объективно указывает характер изменения проявленных свойств соотношения сторон треугольника в зависимости от его вида (Таблица 2 - 4).
Прежде, чем приступить к анализу указанных таблиц, следует обратить особое внимание и напомнить о том, что в соответствии с Принципом Полярности, изменение проявленных свойств любого математического феномена на противоположные, может происходить только в так называемых точках реверса. Эти особые точки, могут присутствовать (восприниматься), либо только в явном, либо только в неявном виде, но никак не одновременно и в том, и в другом виде (либо вообще отсутствовать).
Следует отметить так же тот факт, что в явных (выраженных) точках реверса, проявленное свойство не является ни одним из противоположных в отдельности, а приобретает характер некоего промежуточного значения.
Таблица 2
Для остроугольного треугольника
n = 1 | n = 2 | n > 2 |
a + b > c | a 2 + b 2 > c 2 | a n + b n ? c n |
Из Таблицы 1, 2 очевидно, что при n = 2 не происходит никакого реверса проявленных свойств соотношения сторон остроугольного треугольника.
Следовательно, для любого остроугольного треугольника, возможные точки реверса проявленных свойств соотношения его сторон могут существовать в явном или неявном виде, только при значениях степени, превышающих двойку (n > 2). Либо могут вообще отсутствовать, как таковые.
Таблица 3
Для прямоугольного треугольника
n = 1 | n = 2 | n > 2 |
a + b > c | a 2 + b 2 = c 2 | a n + b n < c n |
Из Таблицы 1, 3 следует, что при n = 2 происходит изменение проявленных свойств соотношения сторон прямоугольного треугольника. И, это изменение происходит не на противоположное свойство, а на некое промежуточное, - выполнение равенства. По всем имеющимся признакам, эта степень и является явной точкой реверса проявленных свойств соотношения сторон прямоугольного треугольника.
Достоверно известно и доказуемо, что не существует никакого другого прямоугольного треугольника, и никаких других степеней, кроме второй, для которых выполнялось бы равенство:
a n + b n = c n .
Следовательно, для прямоугольного треугольника, при n = 2, в явном виде существует только одна единственная точка реверса проявленных свойств соотношения его сторон. Поэтому при n > 2, для любого прямоугольного треугольника, всегда будет справедливым неравенство:
a n + b n < c n .
Здесь необходимо обратить внимание на то, что прямоугольная форма треугольника в явном виде указывает на существование только одной единственной точки реверса проявленных свойств соотношения сторон треугольника.
Это обстоятельство является краеугольным и наиважнейшим в проводимых исследованиях, поскольку четко и ясно указывает на ту область (n = 2), где в явном или неявном виде может присутствовать одна единственная точка реверса проявленных свойств соотношения сторон в любом треугольнике.
Таблица 4
Для тупоугольного треугольника
n = 1 | n = 2 | n > 2 |
a + b > c | a 2 + b 2 < c 2 | a n + b n < c n |
Из Таблицы 1, 4 очевидно, что при n = 2 происходит изменение проявленных свойств соотношения сторон тупоугольного треугольника. Причем, это изменение происходит сразу же на противоположное свойство, минуя какие-либо промежуточные значения. Значит, по всем имеющимся признакам можно заключить, что точка реверса свойств соотношения сторон тупоугольного треугольника является неявной (не выраженной в явном виде). И теперь, этот факт представляется вполне понятным, поскольку в действительности (в явном виде) такой реверс среди всех видов, происходит только у прямоугольного треугольника.
Следовательно, для любого тупоугольного треугольника не существует в явном виде никаких точек реверса проявленных свойств соотношения его сторон, независимо от СТЕПЕНИ.
Вместе с тем, для тупоугольного треугольника, между n = 1 и n = 2, в неявном виде существует очевидная точка реверса проявленных свойств соотношения его сторон. Кроме того, раннее было показано, что неявный реверс проявленных свойств соотношения сторон тупоугольного треугольника, должен быть жестко связанным с единственным явным реверсом (точкой реверса) аналогичных свойств прямоугольного треугольника. Это обстоятельство представляется вполне закономерным, если рассматривать треугольник, как единый и естественный феномен проявленной области Единого математического Мира.
Таким образом, можно сделать достаточно обоснованный вывод о том, что для тупоугольного треугольника существует всего один единственный неявный реверс проявленных свойств соотношения его сторон. Поэтому при n > 2, для любого тупоугольного треугольника, всегда будет справедливым неравенство:
a n + b n < c n .
Подобным образом можно показать, что и для остроугольного треугольника отсутствуют какие бы то ни было точки реверса вообще, поскольку в предполагаемой области возможного реверса (n = 2), таковые не воспринимаются никаким из перечисленных образов (явно или неявно). Значит, учитывая наличие жесткой связи единственного явного реверса проявленных свойств соотношения сторон прямоугольного треугольника, с предположительными реверсами аналогичных свойств остроугольного треугольника, убедительно свидетельствует об отсутствии их, как таковых, в треугольнике подобной формы.
Следовательно, можно заключить, что для любого остроугольного треугольника при n > 2, всегда будет справедливым неравенство:
a n + b n > c n .
В Таблице 5 представлены все результаты проведенных здесь исследований свойств соотношения сторон треугольника.
Таблица 5
n = 1 | n = 2 | n > 2 | |||
Любой | Остроугольн. | Прямоугольн. | Тупоугольн. | Остроугольн. | Прямоугольн. и тупоугольн. треугольник |
a + b > c a + b != c | a 2 + b 2 > c 2 a 2 + b 2 != c 2 | a 2 + b 2 = c 2 | a 2 + b 2 < c 2 a 2 + b 2 != c 2 | a n + b n > c n a n + b n != c n | a n + b n < c n a n + b n != c n |
Эта таблица является практически симметричной, что несомненно создает ощущение объективной естественности и гармонии.
Кроме того, она удивительно красиво и гармонично воплотила (увязала) в себе единство реверсов таких отдельных свойств треугольника, как его формы и соотношения его сторон.
Другими словами, с одной стороны, вторая степень достаточно наглядно (явно) демонстрирует реверс в прямоугольной форме треугольника, в ходе ее изменения от остроугольной к тупоугольной (см. таблицу 1).
С другой стороны, прямоугольный треугольник, так же наглядно демонстрирует реверс в показателе степени (СТЕПЕНИ) соотношения его сторон, при переходе ее значений от единицы до превышающих двойку (см. таблицу3).
Таким образом, оказывается, что точки реверсов разнотипных свойств одного и того же единого объекта (в данном случае, - треугольного представления бесконечной числовой шкалы), способствуют ясному и четкому проявлению друг друга, как бы, подтаскивая или указывая друг на друга.
Именно прямоугольный треугольник, как явная и единственная точка реверса его формообразующего свойства явился своеобразным катализатором решения поставленной задачи о единственности точки реверса проявленных свойств соотношения его сторон.
По сути своей, единственность реверса проявленных свойств формы треугольника (прямоугольный треугольник), является основополагающей посылкой и основой для утверждения о единственности реверса и свойств соотношения степеней его сторон. А этот факт, можно считать подтверждением истинности Великой теоремы Ферма.
Поскольку, удалось обоснованно и логично показать, что вторая степень (n = 2) является не просто точкой реверса проявленных свойств феномена соотношения чисел в зависимости от показателя их степеней, но и единственной такой точкой, то утверждение Пьера Ферма относительно абсолютного выполнения (истинности) неравенства:
a n + b n != c n , при n > 2,
является вполне естественным и гармоничным.
Графически, с использованием образа обычной бесконечной числовой шкалы, феномен Великой теоремы Ферма, может быть представлен в виде, изображенном на рисунке 7.
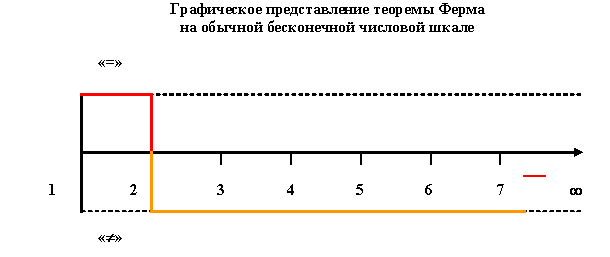
Рис. 7
Явно бросается в глаза очевидная несимметричность подобного графического представления этой теоремы, что дает «привкус» (ощущение) какой-то искусственности, натянутости и неестественности.
Думаю, что возникновение этого эффекта связано с нашим сегодняшним ограниченным представлением о бесконечном числовом пространстве (Едином математическом Мире). Как уже отмечалось раннее, скорее всего, именно введение понятия нуля в это бесконечное числовое пространство и явилось результатом ощущения подобной дисгармонии древними математиками.
Совсем по-другому выглядит графический образ этой теоремы с позиций введенных здесь других представлений о бесконечном математическом пространстве и Едином математическом Мире (рис. 8).
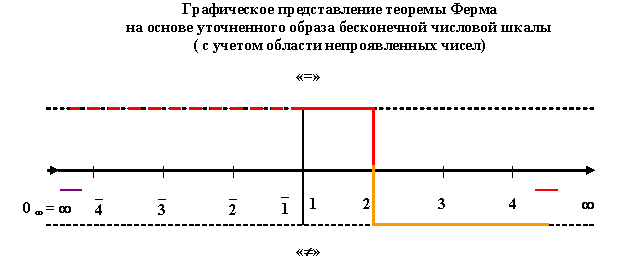
Рис. 8
Такой графический образ теоремы Ферма, представляется уже более симметричным, естественным и гармоничным. Но, все-таки, определенный перекос в симметрии вполне отчетливо наблюдается.
И, здесь, представляется своевременным вспомнить, что «причинами» всех феноменов в проявленной области математического пространства, являются аналогичные феномены с противоположными свойствами в непрявленной области, как, впрочем, и наоборот. В связи с этим важнейшим обстоятельством, графический образ так называемой Единой теоремы Ферма в Едином математическом пространстве (Мире), примет следующий окончательный вид (рис.9).
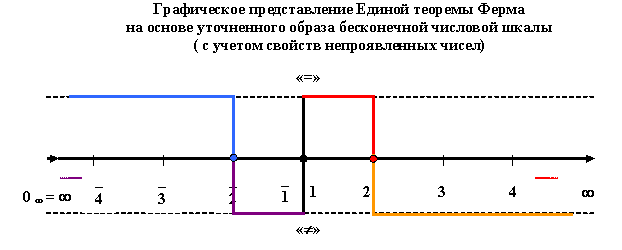
Рис. 9
Такой графический образ Единой теоремы Ферма представляется наиболее естественным и гармоничным в своем единстве, и, кроме того, - наиболее простым и очевидным средством выражения ее внутреннего содержания (сути).
Значит, тот математический феномен, который в виде Великой теоремы Ферма более 350 лет будоражил и сводил с ума огромное множество исследователей, по сути своей, является лишь одной из двух возможных сторон (проявленной и непроявленной), но одной и той же единой «Монеты».
В этом смысле, забавным будет выглядеть Великая теорема Ферма по «ту» сторону проявленного математического пространства, т.е. в области непроявленного математического мира:
_ _ _ _ _ _ _ _
a^^n + b^^n = c^^n , при n > 2 !
В качестве достаточно убедительного подтверждения справедливости последнего (ключевого) из этапов настоящего исследования, можно привести всем известную теорему Пифагора. Эта теорема издавна известна всему человечеству, и является одним из величайших его достижений.
Теорема Пифагора всегда представлялась, как некая объективная математическая данность или закономерность Единого математического Мира, существующая сама по себе. Она не дает никаких разъяснений насчет того, почему именно прямоугольный треугольник, и именно вторая степень величин его сторон, дает столь известное и знаменитое соотношение (равенство):
a 2 + b 2 = c 2 .
Результаты проведенных здесь исследований, позволяют несколько прояснить эту ситуацию, немного приподняв покрывало непостигаемой таинственности математических феноменов.
Дело в том, что теорема Пифагора, по своей сути, является воплощением (выражением) единого реверса известных основных свойств треугольного представления бесконечной числовой шкалы (феномена треугольной формы). Ведь, именно прямоугольный треугольник, а ни остроугольный или тупоугольный, и именно вторая степень суммы двух его катетов, а ни какая бы то ни было другая, ни больше и ни меньше (равна) квадрата его гипотенузы. А точка явного реверса, каких бы то ни было свойств, - это всегда тонкая исключительность и особенность, нехарактерная для масштабных противоположных проявлений этих самых свойств.
Конечно, может быть, не совсем корректной выглядит попытка подтверждения справедливости каких-либо утверждений с помощью фактов, на которых, по сути, и сформированы эти утверждения. Но хотелось бы обратить внимание на то, что используемый подход (технология) в рассуждениях, не ставит перед собой целью подтверждение справедливости теоремы Пифагора, как таковой. Для этой цели существуют другие известные, привычные и простые способы.
Внимание привлекает несколько другой аспект соотношения этих Великих теорем.
И теорема Пифагора, и теорема Ферма являются закономерными соседними звеньями (элементами) одной и той же цепи процесса математического познания, в которой все взаимосвязано (Едино).
В этом контексте, теорема Пифагора является естественной первоначальной ступенью на пути решения проблем, связанных с теоремой Ферма. Вместе с тем, успешное разрешение теоремы Ферма, дает возможность понять некий другой, раннее неизвестный и незаметный смысл (суть) теоремы Пифагора, который я и попытался здесь очень кратко показать.
Этот удивительный факт поражает воображение, и может послужить в качестве толчка к неким серьезным исследованиям вопросов методологического обеспечения процесса познания.
Кстати, если я не ошибаюсь, то знаменитую формулировку своей теоремы Пьер Ферма написал на полях книги Диофанта «Арифметика», как раз напротив изложения материалов, связанных с теоремой Пифагора.
К одному из ценных достоинств Великой теоремы Ферма можно отнести тот факт, что она стала воплощением, пожалуй, одной из первых попыток математического исследования так называемого «неисключенного третьего» в логике. Наверное, позволительно сказать, что эта теорема является своеобразной родоначальницей «нечеткой логики», правомерность и эффективность использования которой, по-моему, совершенно очевидны.
Как ни стыдно в этом признаться, но мне практически ничего не известно о Пьере Ферма, как ученом – математике, ввиду своей значительной удаленности от этой области научных знаний. Тем более, мне не известен Пьер Ферма, как человек, впрочем, этим недостатком обладали и обладают все исследователи, и, вряд ли, такое положение дел как-то поправимо.
Мне кажется, что вызвало бы меньшее удивление, если бы автором этой теоремы оказался кто-нибудь из древних выдающихся математиков, например, Пифагор или Диофант, на полях книги которого («Арифметика»), Ферма записал (изложил) свою Великую теорему. Такое авторство представляется более вероятным, поскольку именно древние математики, более, чем кто-либо после них, были склонны придавать числам и арифметике в целом, некий метафизический, мистический и религиозный (божественный) смысл, т.е. смысл, скрывающийся от обычного взгляда под внешней формой.
Первым впечатлением, после проведенных исследований теоремы, было ощущение того, что, так или иначе, но Ферма обладал неким необычным универсальным знанием закономерностей Единого математического Мира. Невозможно сказать точно, были ли эти знания, результатом его какого-то особого понимания, приобретенного им индивидуально и самостоятельно, или же он заимствовал их у кого-то, обладавшего таким пониманием и оставшегося в тени истории развития науки.
Однако, после наиболее общего ознакомления с кругом интересов и обширным полем успешной деятельности этого, несомненно, выдающегося мыслителя и исследователя, наиболее вероятным представляется все же первый вариант. Скорее всего, сам Ферма являлся источником и носителем некоего удивительного понимания единых закономерностей математического мира. Хотя, при всем этом, можно допустить определенную долю вероятности того, что к своей теореме Ферма пришел интуитивно, или в какой-то степени случайно.
Мне кажется, что свое, никому не известное, доказательство теоремы, которое он назвал «чудесным», и является тем самым другим скрытым, более важным ее содержанием, которое было охарактеризовано здесь, как очень удачная, красивая и простая математическая трактовка глобального и универсального принципа Единого Мироздания, - Принципа Полярности.
Кроме того, думаю, что говоря о невозможности написания «чудесного» доказательства своей теоремы на полях книги Диофанта, из-за их узости, Ферма, на самом деле, высказывался, таким образом, об ограниченности (узости) наших обычных и привычных представлений о Едином Мироздании и его отдельных феноменах, которые являются неизбежным следствием нашего образа мышления и логики.
Возможно, именно по этой причине, он и не оставил потомкам своего знаменитого, таинственного и чудесного доказательства своей Великой теоремы, поскольку опасался быть непонятым.
Я заранее согласен с любой оценкой моей работы
Пусть каждый исследователь, сумевший и нашедший в себе силы дочитать до конца, этот мой далеко несовершенный продукт около научного и около публицистического творчества, сам определяет и решает для себя, каким образом воспринимать представленные здесь материалы. И, воспринимать ли их вообще.
Главное, чтобы в процессе этого самоопределения, каждый из них сумел не пойти на поводу собственной лени и автоматической привычки подменять всякую индивидуальную (самостоятельную) мыслительную деятельность, подражанием другим людям, пусть даже очень выдающимся.
Как уже отмечалось раннее, проведенные исследования, рассматривались, как конкретный своеобразный эксперимент, подтверждающий истинность, универсальность и эффективность неких глобальных принципов (законов) Единого Мироздания, издревле известных человечеству.
Единственным побуждающим мотивом к написанию этой работы, а так же ее главной целью, считаю, - обратить внимание, привлечь взгляд и заинтересовать профессиональных ученых, а так же самых разнообразных исследователей (мыслителей) к той, другой стороне человеческого понимания и знаний, которые совершенно незаслуженно и в силу каких-то немыслимых обстоятельств, остались за пределами нашего обычного (привычного) мировосприятия и миропредставления, автоматический и неосознанный характер которых, придает им привкус (ощущение) объективной реальности и без альтернативности.
Думаю, что для большинства исследователей не будет составлять особого труда, суметь увидеть и рассмотреть тот «мост», который соединяет мир математический с Единым Мирозданием (той объективной реальностью, которая всех нас окружает, или лучше – объединяет). По сути своей, Единый математический Мир является обозримым и наиболее достоверным образом (отражением) Единого Мироздания, которые отличаются лишь количеством, качеством и разнообразием проявляемых феноменов и их свойств. Можно даже сказать, что математический мир является упрощенной, своеобразной одномерной моделью многомерного (в феноменологическом смысле) Единого Мироздания.
Поэтому, тот подход (методология или технология), который был использован для проведения исследований отдельного феномена математического мира, будет вполне применимым и для подобных исследований разнообразных феноменов физического мира.
По моим, вполне обоснованным представлениям, уже сегодня с позиции продемонстрированной методологии (нетрадиционных и непривычных знаний), можно успешно разрешить целый ряд совсем непростых проблем современной науки. Нет смысла перечислять сейчас и здесь все эти проблемы, по которым уже имеется ряд некоторых интересных и неожиданных наработок. К тому же, не хотелось бы предоставлять кому-либо возможность уличить меня в наглости, высокомерии, самоуверенности, а так же, возможно, и в каких-то психических заболеваниях. Короче, во всех тех пороках, которые в той или иной степени, но присущи нам всем без исключений, и, которые мы, в подавляющем большинстве случаев, способны видеть у кого угодно, кроме себя родимого.
Практически большинство проблем, имеющихся и возникающих в любых областях познавательной деятельности человека, можно успешно решить с указанных позиций. Для этого достаточно лишь обрести соответствующее понимание неких глобальных и универсальных закономерностей Единого Мироздания, а так же суметь направить острие своего внимания на интересующие вопросы (проблемы).
Необходимо обратить особое внимание на то, что здесь речь идет именно об обретении понимания, т.е. некоего индивидуального состояния разума (сознания), содержащего в себе громадный (практически неограниченный) потенциал по приобретению новых знаний. Это понимание не является каким-то алгоритмом или инструкцией по познавательной деятельности, его невозможно выучить, или приобрести извне каким-либо другим путем. Оно приобретается только самостоятельно и индивидуально, и только в результате предпринятых определенных усилий (сверх усилий), направленных на его достижение в себе самом.
В завершение этой работы, хочу и должен признаться перед самим собой в том, что длительное время неосознанно заблуждался относительно наличия какой-либо объективной связи между математическим и физическим миром. Более того, пребывая в этом своем заблуждении, я совершенно был убежден в том, что такой связи нет и быть не может.
То, с чем я столкнулся, исследуя Великую теорему Ферма, совершенно неожиданно и полностью перевернуло все мои представления о роли и месте математической науки в едином процессе познания Мироздания.
Сегодня могу сказать со всей откровенностью и уверенностью, на которую способен, что я ошибался, и ошибался в силу своей привычки, - совершенно необоснованно, автоматически и неосознанно приобретать уверенность в том, чему лишь не сумел рассмотреть (увидеть) альтернативу.
Поэтому, я очень рад, что удалось перешагнуть через эту свою уверенность, и изменить свои представления о математической науке. Но эти изменения совсем не являются тривиальным переходом от одного из двух противоположных представлений, к другому. Скорее всего, этот процесс напоминает переход от одного из крайних противоположных представлений в некую серединную область, так называемую точку реверса. Думаю, что именно с позиции этой точки реверса, единственно и возможно обеспечить столь необходимые естественность и объективность нашего восприятия и представлений о Едином Мироздании.
Современные математические представления, так же далеки от обычного физического мира (объективной реальности), как и от естественного и объективного (Божественного) Единого математического Мира. И, такое положение математической науки является, отнюдь, не исключительным и уникальным. Такое же положение дел характерно и для физической науки, и для всех других наук, поскольку, по сути, все они основаны (базируются) на одних и тех же единых и субъективных представлениях человека об окружающем его мире.
Ведь человек, пытающийся познавать окружающий его Мир, в конечном счете, познает самого себя!
В этой работе я попытался показать другие, естественные и объективные представления о Едином Мироздании, которые может сформировать в себе практически любой исследователь, окончательно не утративший способность к самостоятельному мышлению и который готов к такой работе над собой.
У меня есть необъяснимое ощущение уверенности в том, что обязательно найдутся исследователи, по крайней мере, хотя бы один, которому и адресованы все мои ничтожные мыслительные и писательские потуги. Так или иначе, но сегодня я сделал все, что было в моих силах для достижения поставленной перед собой задачи.
Примечание: Я в курсе того, что теорема Ферма доказана американцем Вилсом (если не ошибаюсь), и математическая общественность признала это доказательство. Однако, мне кажется, что сам Ферма располагал другим, более простым и оригинальным доказательством своей теоремы.
Литература:
[1] Кибалион ( можно ознакомиться здесь - http://vmihail33.chat.ru/cod.htm)